ANGULO RECTO
Un ángulo recto es aquel que mide 90° (sexagesimales). Su amplitud medida en otras unidades es: π/2 radianes y 100g (centesimales). Sus dos lados son dos semirrectas perpendiculares, y el vértice es el origen de dichas semirrectas.
En Geometría, al respecto del ángulo recto podemos destacar las siguientes consideraciones :
_ Un triángulo rectángulo tiene un ángulo recto.
_ Un cuadrado tiene cuatro ángulos rectos.
_ Dos ángulos rectos forman un ángulo llano o plano, es decir, de 180°.
_ Cuatro ángulos rectos forman un ángulo completo o perigonal, es decir, de 360°.
_ Dos diámetros ortogonales de una circunferencia la dividen en cuatro cuadrantes; sus prolongaciones conforman cuatro ángulos rectos con vértice en el centro, cuyas amplitudes suman 360°.
En Geometría, al respecto del ángulo recto podemos destacar las siguientes consideraciones :
_ Un triángulo rectángulo tiene un ángulo recto.
_ Un cuadrado tiene cuatro ángulos rectos.
_ Dos ángulos rectos forman un ángulo llano o plano, es decir, de 180°.
_ Cuatro ángulos rectos forman un ángulo completo o perigonal, es decir, de 360°.
_ Dos diámetros ortogonales de una circunferencia la dividen en cuatro cuadrantes; sus prolongaciones conforman cuatro ángulos rectos con vértice en el centro, cuyas amplitudes suman 360°.
TEOREMA DE PITAGORAS
Desde la época de los sumerios se conocía una propiedad de los triángulos que hoy conocemos como teorema de Pitágoras.
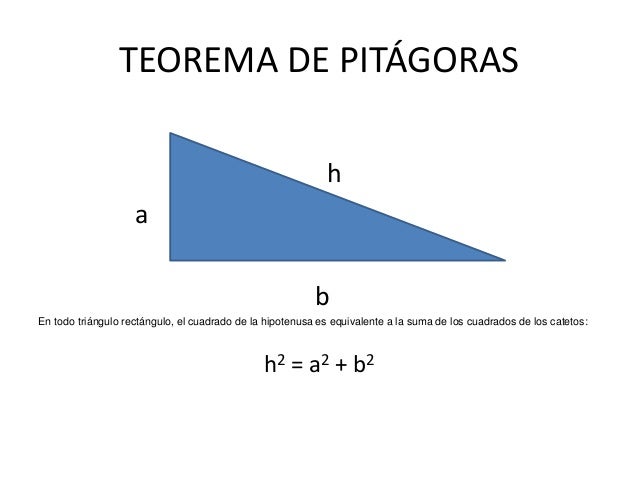
Teorema de Pitágoras
En un triangulo rectángulo Si a y b son las longitudes de los catetos de un triángulo rectángulo y c es la longitud de la hipotenusa, entonces la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa. Esta relación está representada por la fórmula: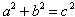
En un triangulo rectángulo Si a y b son las longitudes de los catetos de un triángulo rectángulo y c es la longitud de la hipotenusa, entonces la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa. Esta relación está representada por la fórmula:
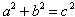
Euclides demuestra este teorema en la proposición 47 del primer libro de "Los Elementos" y a continuación demuestra el recíproco que puede enunciarse así:
Si en un triángulo cualquiera, el cuadrado del lado mayor es igual a la suma de los cuadrados de los otros dos lados, entonces uno de los ángulos del triángulo es recto.
demostración geométrica del Teorema de Pitágoras
A = área del cuadrado de lado a+b
A = (a+b)^2 = a^2 + 2ab + b^2
A = (a+b)^2 = a^2 + 2ab + b^2
Ac = Área del cuadrado de lado c
At = Área del triangulo rectángulo de catetos a y b
A = Ac+4At.
At =(1/2)ab
A = c^2+2ab
a^2 + 2ab + b^2 = c^2 + 2ab
a^2 + b^2 = c^2
TERNAS PITAGÓRICAS
Una terna pitagórica consiste en una tupla de tres enteros positivos a, b, c que cumplen que a² + b² = c². El nombre deriva del teorema de Pitágoras, el cual plantea que en cualquier triángulo rectángulo, se cumple que x² + y² = z² (siendo x e y las longitudes enteras de sus catetos y z la de la hipotenusa).
En sentido contrario también se cumple, o sea, cualquier terna pitagórica se puede asociar con las longitudes de dos catetos y una hipotenusa, formando un triángulo rectángulo
La primera de las ternas pitagóricas es 3,4,5
LA GEOMETRIA
La geometría es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio: puntos, rectas, planos, politopos . y los elementos que forman, es decir paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc.).
Es la base teórica de la geometría descriptiva o del dibujo técnico.
ARTÍCULOS RELACIONADOS
LA GEOMETRIA
Artes Liberales. Geometria et Euclides.
This work is in the public domain in its country of origin and other countries and areas where the copyright term is the author's life plus 100 years or less.
EL REPLANTEO
EL TIRO DE CUERDAS
El replanteo consiste en pasar las medidas del plano a la obra.
Existieron y existen compases, escuadras, y cartabones, plomadas y niveles , grandes para la Obra que estaban en manos del maestro, para el trazado en el lugar de pequeñas geometrías y para la comprobación de las trazas replanteadas.
Compás de Obra escuadra, plomada, y nivel de obra
Enrique III junto al Maestro de Obras con su cartabón según "La Vida de los Santos Albano y Amfíbalo".
LAS ESTACAS Y LA CUERDA
Existiendo estas piezas básicas, las herramientas principales en obra para el trazado de geometrías a escala real han sido y son la cuerda y las estacas. Con las estacas se fijan puntos y con la cuerda se trazan los trazos rectos y las curvas del compas.
EL REPLANTEO
del Angulo recto en Obra
del Angulo recto en Obra
El trazado del Angulo recto en geometría y en dibujo técnico arquitectónico fue un asunto pronto dominado por los geómetras y ejecutores de planimetrías. Los egipcios ya conocieron los secretos de su trazado, y Pitágoras estableció sus reglas en el saber clásico.
En los tableros de dibujo se disponía de herramientas de dibujo que permitían su realización: La regla y compás, y por ello la escuadra, el cartabón, asi que en los planos la ejecución de ángulos rectos era inmediato.
El replanteo en el lugar del ángulo recto en planta ha sido a lo largo de la historia una manifestación de la capacidad técnica de los maestros constructores.
Hemos de reparar en que en las construcciones populares antiguas, en los lugares menos accesibles y para los usos menos importantes, la construcción de las edificaciones carecen de ángulos rectos , como mucho pueden verse aproximaciones a los mismos.
En obra las trazas geométricas del ángulo recto es una manifestación de la capacidad técnica de los maestros constructores
Replanteo por mediana
replanteo por triangulo 3.4.5
TRIANGULO RECTANGULO
TRIANGULO RECTANGULO
LA CUERDA DE DOCE NUDOS
Desde tiempos inmemoriales la utilización de esta cuerda como unidad de medida era ampliamente conocida y aplicada. Como indican algunos autores tanto el templo de Karnak (Egipto), como Stonehenge (Reino Unido) fueron construidos a partir de su utilización.
Los egipcios, conocedores de la propiedad geométrica del triangulo rectangulo, utilizaron con anterioridad a Pitagoras una cuerda dividida en doce partes iguales. Marcaban las partes mediante nudos y al estirar de tres de ellos para formar un triángulo de lados 3, 4 y 5, obtenían el ángulo recto que necesitaban para la construcción de las pirámides
La cuerda de 12 nudos ha sido fundamental para el replanteo en el terreno de las trazas ortogonales, para el replanteo del ángulo recto en el terreno, a lo largo de los siglos.
Puede decirse que todo constructor debía disponer de una de ellas entre sus instrumentos de trabajo.
Para que la cuerda fuera precisa y no se viera alterada por cambios de temperatura o humedad se mezclaba cera y resina y se impregnaba la cuerda con esta mezcla, dejándola luego colgando con un peso en el extremo inferior, a punto para iniciar cualquier otra medición.
SISTEMA DUODECIMAL
La cuerda de 12 nudos incide en la relación histórica de la construcción y la arquitectura con el sistema de medidas duodecimal.
Los apóstoles (12) y la cuerda (de doce nudos) en una iluminación medieval.
San Pedro, San Pablo y San Esteban se aparecen en sueños al Abad Gunzo de Cluny.
Con una cuerda le enseñan el esquema de la abadía que construirá
Miniatura del s. XII. Paris .Biblioteca Nacional du Colombier.
La cuerda de doce nudos complementa el numero de vínculos del sistema de medida duodecimal en el mundo de la arquitectura y de la construcción histórica.
La importancia de la "cuerda de nudos" fue recogida en los blasones eclesiásticos, asignandose al obispo el timbre de una cuerda de 12 nudos.
Articulo relacionado:
SISTEMA DE MEDIDA DUODECIMAL
Lógicamente todos estas herramientas básicas del maestro constructor forman parte de la simbología de las Logias.
